Temperaturen in und auf der Wand
.
Als Anlagenmechaniker hat man wohl kaum Einfluss auf den Aufbau der Außenwände eines Hauses. Und doch ist es hochinteressant wie der Wandaufbau sich auf das Haus und den Wohnkomfort auswirkt. Man kann auch einige Phänomene mit Kenntnis dieser Zusammenhänge besser begreifen.
.
Der Aufbau einer Außenwand ist entscheidend für deren R-Wert und damit für den U-Wert. Der R-Wert beschreibt den Widerstand, der der Wärme, die verschwinden will, entgegengesetzt wird. Je dicker die Schichten von Innenputz, Mauerwerk, Dämmung und Außenputz, desto größer ist dieser Widerstand, der R-Wert eben. Je größer der R-Wert ist, desto kleiner ist der Wärmedurchgangskoeffizient, den man als U-Wert bezeichnet. In der Praxis hat sich umgangssprachlich der U-Wert als Bezeichnung für die Dämmeigenschaften einer Wand verbreitet.
.

.
Wenn Wärme wandert
Der U-Wert mit seiner Einheit W/(m²K) gibt an, wie viel Leistung (in Watt) pro Fläche (in Quadratmeter) pro Grad Temperaturdifferenz (in Kelvin) ausgetauscht wird. Beispielsweise geben zehn Quadratmeter Außenwand eines Raumes mit 20 °C Innentemperatur an eine minus 10 °C kalte Umgebung Wärme ab. Je nach U-Wert „wandern“ dann:
.
U-Wert = 0,25 W/(m²K) → 75 Watt
U-Wert = 0,5 W/(m²K) → 150 Watt
U-Wert = 1,0 W/(m²K) → 300 Watt
U-Wert = 2,0 W/(m²K) → 600 Watt
.
Über eine Außenwand mit einem U-Wert von 0,25 W/(m²K) geht also deutlich weniger Energie flöten als über eine Außenwand mit einem U-Wert von 2,0 W/(m²K). Der R-Wert dieser aufgeführten U-Werte ist der so genannte Kehrwert, also:
.
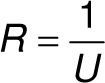
.
Ein U-Wert von beispielsweise 2,0 W/(m²K) ergibt einen R-Wert von 0,5 (m²K)/W. Um die beiden voneinander abhängigen Werte berechnen zu können, kann man die Dicke einzelner Schichten des Wandaufbaus betrachten. Je dicker das Mauerwerk oder die Dämmung, desto größer der R-Wert und desto kleiner der U-Wert.
.
Dick alleine reicht nicht
Die Dicke der Schichten alleine ist natürlich nicht das Maß aller Dinge. Wichtig ist es auch, ob die jeweilige Schicht die Wärme gut oder schlecht leitet. Rein rechnerisch ergibt sich dieser Widerstand „R“ also aus der Dicke, geteilt durch die Leitfähigkeit.
.

.
Die Bedeutung der Variablen:
R: Widerstand der Schicht einer Wand in m²K/W
d: Dicke einer Schicht in Meter
λ: Wärmeleitfähigkeit einer Schicht in W/(m K)
.
.
Prüft man diese Formel nach dem Inhalt der eben beschriebenen Behauptungen, ist die Logik ebenfalls hergestellt. Je größer der Wert über dem Bruchstrich (die Dicke), um so größer das Ergebnis (Widerstand). Und je kleiner der Wert unter dem Bruchstrich (Leitfähigkeit), desto größer das Ergebnis (Widerstand). Dann sind noch einige Widerstände als feste Werte anzunehmen; die Wärmeübergangswiderstände:
.
Wärmestrom aufwärts:
Rsi = 0,10 m²K/W
.
Wärmestrom horizontal:
Rsi = 0,13 m²K/W
.
Wärmestrom abwärts:
Rsi = 0,17 m²K/W
.
Wärmestrom nach außen:
Rse = 0,04 m²K/W
.
Die komplette Formel zur Ermittlung des gesamten Widerstandes „RT“ für eine Anzahl von Schichten ergibt sich aus:
.
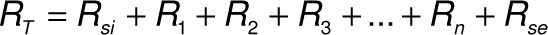
.
Umgangssprachlich sagt diese Formel aus: Die Addition aller Einzelwiderstände ergibt den Gesamtwiderstand.
.
Die klassische Außenwand
Um das Gefühl für einen konkreten Wert zu bekommen sei eine klassische Außenwand mit folgenden Schichten gegeben, aufgezählt von innen nach außen:
.
Schicht 1:
1,2 cm Gipskarton mit
λ-Wert von 0,25 W/(mK)
.
Schicht 2:
24 cm Kalksandstein mit
λ-Wert von 0,50 W/(mK)
.
Schicht 3:
10 cm Wärmedämmung mit
λ-Wert von 0,030 W/(mK)
.
Schicht 4:
2,0 cm Außenputz mit
λ-Wert von 0,10 W/(mK)
.
Die Werte werden gesammelt:
Rsi = 0,13 m²K/W (horizontal)
.
Für Schicht 1 gilt:
.

.
Für Schicht 2 gilt:
.
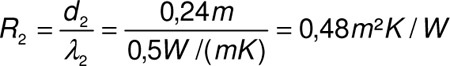
.
Für Schicht 3 gilt:
.

.
Für Schicht 4 gilt:
.

.
Rse = 0,04 m²K/W (außen)
.
Die Addition der Widerstände ergibt den Gesamtwiderstand:
.
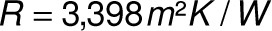
.
Der Widerstand Wärme abzugeben beträgt also 3,398 m²K/W.
.
Der Kehrwert des Wärmedurchlasswiderstandes ergibt den U-Wert.
.
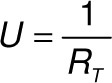
.

.
Entscheidend für die folgenden Schlüsse und gedanklichen Verrenkungen bleiben die Widerstände der einzelnen Schichten.
.
.
Die Schlüsse hieraus
Um mit den gesammelten Daten etwas Sinnvolles anzustellen sollen folgende Vorgaben gelten:
.
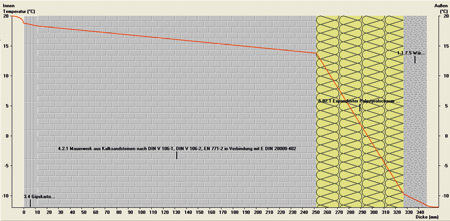
- Innerhalb eines Raumes wird eine Temperatur von 20 °C gehalten. Draußen ist es abgekühlt auf minus 12 °C.
- Der Temperaturverlauf innerhalb der Wand soll berechnet werden. Die Frage stellt sich also, wo die Temperatur um wie viel Grad sinkt, um von 20 °C auf minus 12 °C abzunehmen. Dazu werden nun die Widerstände einzeln betrachtet.
.
Der erste Widerstand, immer ausgehend vom Raum nach draußen, ist der Wärmeübergangswiderstand von 0,13 m²K/W. Bezogen auf den Gesamtwiderstand der Wandkonstruktion beträgt das Verhältnis des Innenwiderstandes:
0,13 / 3,398 = 0,038 (3,8 %)
.
Der nächste Widerstand ist der Innenputz und erzeugt ein Verhältnis von:
0,048 / 3,398 = 0,014 (1,4 %)
.
Es folgt der Kalksandstein mit:
0,48 / 3,398 = 0,141 (14,1 %)
.
Jetzt erreicht man den höchsten Widerstand mit dem zahlenmäßig größten Verhältnis, die Dämmung:
2,50 / 3,398 = 0,736 (73,6 %)
.
Der Außenputz folgt mit:
0,20 / 3,398 = 0,059 (5,9 %)
.
Der Letzte Widerstand ist wiederum der Übergangswiderstand außen und daher ergibt sich das Verhältnis:
0,04 / 3,398 = 0,012 (1,2 %)
.
Die Prozentangabe hinter den Verhältnissen ist ein Maß für die Abkühlung von 20 °C auf -12 °C. Die Gesamttemperaturdifferenz beträgt 32 Kelvin und gemäß den Einzelwiderständen teilt sich der Temperaturabfall in der Wand auf:
.
.
Innenwiderstand:
3,8 % von 32 K = 1,22 K
.
Innenputz:
1,4 % von 32 K = 0,45 K
.
Kalksandstein:
14,1 % von 32 K = 4,50 K
.
Dämmung:
73,6 % von 32 K = 23,6 K
.
Außenputz:
5,9 % von 32 K = 1,89 K
.
Außenwiderstand:
1,2 % von 32 K = 0,38 K
.
Für das leichtere Verständnis werden die Temperaturdifferenzen und der resultierende Verlauf in Bild 2 dargestellt.
.
Wozu so ein Aufwand?
Der R-Wert bleibt der R-Wert und der U-Wert folglich ebenfalls der U-Wert, egal wie die Temperatur in der Wand verläuft. Soviel steht fest: Der R-Wert ändert sich auch nicht, wenn man die Schichten vertauscht, denn der Gesamtwiderstand bleibt ja derselbe. Nur wie verhält es sich nach diesen Erkenntnissen, wenn Schichten verschoben werden? Wenn man beispielsweise die Dämmung zum Raum packt und den Kalksandstein nach außen? Diese Verteilung der Schichten ist in Bild 3 dargestellt. Der Temperatursturz von rechnerisch 23,6 K findet weiterhin in der Dämmung statt. Damit ist der Kalksandstein für den Innenraum speichertechnisch plötzlich aus dem Rennen. Seine nun sehr niedrige Temperatur teilt sich nicht mehr als Wärmespeicher dem Raum mit. Die Dämmung auf der Innenseite der Außenwand lässt den schweren und teuer erkauften Stein eine eher untergeordnete Rolle für das Raumklima spielen. Nebenbei hat er in dieser Anordnung auch kaum Gelegenheit als Feuchtespeicher regulierend auf das Raumklima einzuwirken. Es ist also kein Zufall dass der Aufbau einer Außenwand ist, wie er ist, nämlich Dämmung nach außen und den massigen Kalksandstein nach innen. Auch sieht man die nachträgliche Innendämmung von Häusern immer noch sehr kritisch, unter anderem aus den gezeigten Gründen.
.

.
Weitere Erkenntnisse?
Diese Zahlenspielchen lassen noch einen weiteren Schluss zu: Wenn sich also abhängig von den Widerständen unterschiedliche Temperaturen ergeben, dann müssten sich auch in der Umkehrung von den Temperaturen die Widerstände bestimmen lassen. Und dies ist natürlich den Softwareherstellern bekannt, die entsprechende Berechnungen vorsehen und dem Anwender anbieten. Auch Messgeräte sind aufgrund dieser Gesetzmäßigkeiten in der Lage, einen U-Wert durch Temperaturmessung zu ermitteln. Der praktische Nutzen der eben gezeigten mathematischen Anstrengungen ist damit also auch noch aufgezeigt. Ein klassisches Beispiel ist die alte Jugenstil-Villa im noblen Vorort. Um hier einen U-Wert zu ermitteln, kann man schlecht an der Fassade rumhämmern um Einblick in den Schichtaufbau zu bekommen. Auch eine Kernbohrung verbietet sich hier aus optischen Gründen. Eleganter wirkt es da schon, wenn das Messköfferchen die U-Werte hinreichend genau ans Licht befördert, zerstörungsfrei versteht sich.
.
.
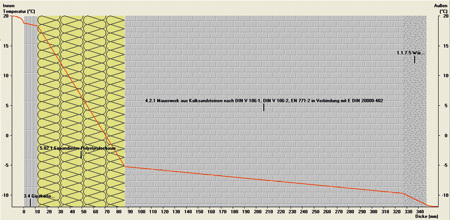
Wie jetzt, U-Wert messen?
Zwei Wände mit ein und derselben Wanddicke können wegen des unterschiedlichen Schichtaufbaus völlig unterschiedliche R-Werte und damit U-Werte haben. Charakteristisch für den R-Wert ist letztlich die gemessene Oberflächentemperatur. Und die lässt damit Rückschlüsse auf das Innenleben der jeweiligen Wand zu. Wohlgemerkt nur auf den Gesamtwiderstand, nicht auf einzelne Schichten. Die Bilder 4 und 5 stellen zwei Wände dar, die sich jeweils mit gleicher Wanddicke präsentieren. Für diesen Vergleich sind wiederum 20 °C als Innen- und minus 12 °C als Außentemperatur angenommen worden. Würde man mittels Messgeräten den Wänden auf den U-Wert fühlen, so würde man zwei unterschiedliche Temperaturen auf der Oberfläche messen können. Die Wand ohne Dämmung wäre deutlich kühler (ca. 15 °C) als jene mit Dämmung (ca. 19 °C). Die R-Werte und damit die U-Werte differieren entsprechend. Obwohl also die Innentemperatur des Raumes auch bei minus 12 °C Außentemperatur auf mollige 20 °C gehalten werden, kann die Oberflächentemperatur der Außenwand unterschiedlich sein. Ein krasses Beispiel kann man bei einer Einscheibenverglasung aus grauer Vorzeit des letzten Jahrtausends noch ausmachen. Obwohl Räume auf 20 °C beheizt sind, können sich Eisblumen auf der Innenseite von solchen Fenstern bilden. Die Älteren unserer Leserschaft werden sich vielleicht noch erinnern.
.
Viele Gesetze der Physik kann man anhand praktischer Erfahrungen belegen. Der Zusammenhang zwischen Dämmung und Wandaufbau ist recht logisch und sogar rechnerisch nachweisbar. Zwar muss man in der Praxis nicht ständig mit Formeln hantieren können, aber die eben ausgeführten Zusammenhänge lassen sich bei einigem Nachdenken recht gut verinnerlichen. Denken Sie doch mal während einer Fahrpause im nächsten Verkehrsstau darüber nach.






