Widerstand in der Wand
.
Gerade wenn es darum geht den U-Wert eines Bauteils zu bestimmen, braucht man ihn, den Durchblick. Nicht nur durch Formeln und Zusammenhänge sondern auch durch das jeweilige Bauteil.
.

.
Der U-Wert - oder lang gesprochen der Wärmedurchlasskoeffizient - in der Einheit W/(m²K) ist für Architekten, Bauherren, Anlagenmechaniker und viele andere am Bau oder Umbau eines Hauses beteiligte Menschen ein interessante Größe. Gibt doch dieser Wert Aufschluss über eine Leistung in Watt (W) bezogen auf einen Quadratmeter (m²) sowie bezogen auf eine Temperaturdifferenz in Kelvin (K) von einem Grad. Der U-Wert gibt also schlichte Auskunft darüber, welche Leistung, z. B. an einer Außenwand, je Quadratmeter abgegeben wird, wenn innen eine Temperatur von z. B. 20 °C und außen eine Temperatur von 19 °C herrschen.
.
Ab durch die Wand
Wird einer Wand beispielsweise ein U-Wert von 1 W/(m²K) zugeordnet, geht durch einen Quadratmeter Fläche ein Watt Energie hindurch, wenn die Temperaturdifferenz der Wandoberflächen ein Kelvin beträgt. Beträgt die Wandfläche aber nicht einen, sondern z. B. fünf Quadratmeter, ist es nicht schwer, den Energiedurchgang für diese Wandfläche festzulegen. Und in Anlehnung an diese Aussage kann man statt einer Temperaturdifferenz von nur einem Kelvin (20 °C auf 19 °C) auch eine Aussage treffen, welche Leistung denn wohl bei 30 Kelvin Differenz abgegeben wird, z. B. bei einer Zimmertemperatur von 20 °C und einer Außentemperatur von -10 °C.
Beispiel:
1W/(m²K) · 5 m² · 30 K = 150 W
An dieser Wand würden also 150 Watt Leistung abgegeben. Aber wen stört es? Zuerst einmal wird sich kaum einer beim Eintritt in ein Gebäude nach dessen U-Werten erkundigen. Spätestens aber im Winter ist der Hausbesitzer froh, wenn sein Häuschen nicht den eben berechneten U-Wert von 1 W/(m²K) für die Außenwand besitzt. Er freut sich, wenn stattdessen ein U-Wert von beispielsweise 0,5 W/(m²K) sein Haus gegen Auskühlung schützt. Verglichen mit dem ersten Berechnungsbeispiel macht ein um 0,5 W/(m²K) geringerer U-Wert schon ordentlich was aus.
Gegenprobe:
0,5 W/(m²K) · 5 m² · 30 K = 75 W
An diesen Außenwänden würde nur noch die Hälfte an Wärme verloren gehen. Der Hausbesitzer oder jener, der ein Häuschen errichtet oder kauft, ist an guten (folglich kleinen) U-Werten interessiert. Die Planer, also Architekten, Bauingenieure, Statiker, und die Handwerker am Bau wie Maurer, Zimmerleute oder eben Anlagenmechaniker, müssen mit den jeweiligen U-Werten umgehen oder eben eigene Leistungen darauf abstimmen. Der Anlagenmechaniker stimmt die Heizungsanlage auf diese U-Werte ab. Vermeintlich schlechte U-Werte führen beispielsweise zu der Auslegung von relativ großen Heizkörpern. Topp-U-Werte eines Niedrigenergiehauses machen nur relativ kleine Heizflächen nötig. Über viele Jahre ein Haus, das „schlechte“ U-Werte aufweist zu beheizen, ist kostenintensiver als die gleiche Wohnfläche in einem Haus mit sehr guter Wärmedämmung zu temperieren. Dieser Zusammenhang wird für den Otto-Normal-Verbraucher angesichts steigender Energiepreise immer interessanter.
.
.
Wie wird’s gerechnet?
Die Berechnung des U-Wertes ist nur auf den ersten Blick fremd. Hat man die Grundzüge verstanden, ist man in der Lage zum Teil schon per Kopfrechnung Überschlagswerte auszuspucken.
Die Grundformel zur Entwicklung des U-Wertes lautet:

.
Der U-Wert ergibt sich also aus dem Kehrwert des Wärmedurchlasswiderstandes RT.
Aber wie errechnet sich dann RT? Für diesen Wert gilt folgende Gleichung:

.
Umgangssprachlich könnte man sagen: Addiere alle Einzelwiderstände zu einem Gesamtwiderstand (RT) auf. Die Einzelwiderstände setzen sich zusammen aus dem ersten (Rsi) und letzten (Rse) vom gleichen Typ, sowie die „Schichtwiderstände“ 1 (R1) bis zur letzten (n-ten) Schicht (Rn). Die als Übergangswiderstände bezeichneten Rsi und Rse ergeben sich aus Tabellen.
Für Rsi, also den inneren Übergangswiderstand, sind nur drei Werte relevant. Je nach Wärmestrom ergeben diese sich wie folgt:
▲ Für den Wärmestrom aufwärts gilt: Rsi = 0,10 m²K/W (beispielsweise an einer Decke)
► Für den Wärmestrom horizontal gilt: Rsi = 0,13 m²K/W
(beispielsweise an einer Außenwand)
▼ Für den Wärmestrom abwärts gilt: Rsi = 0,17 m²K/W
(beispielsweise an einem Fußboden)
.
Für Rse also den externen (äußeren) Übergangswiderstand gilt:
Rse = 0,04 m²K/W
Es fehlen als letzte Größen also nur noch R1 bis Rn. Hierfür sieht es formeltechnisch so aus:
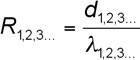
.
Das heißt: Dicke der betrachteten Schicht geteilt durch den Lambda-Wert dieser Schicht ergibt den Widerstand der jeweiligen Schicht. Die Dicke der Schicht lässt sich ja noch ausmessen oder irgendwie bestimmen. Aber was hat es mit dem Lambda-Wert (λ-Wert) auf sich? Der Lambda-Wert gibt Aufschluss über die Wärmeleitfähigkeit eines Stoffes. Gute Wärmeleiter wie Kupfer haben einen Lambda-Wert von beispielsweise 380 W/(mK) Dem gegenüber hat eine gebräuchliche Isolierung einen Wert von 0,035 W/(mK).
.

.
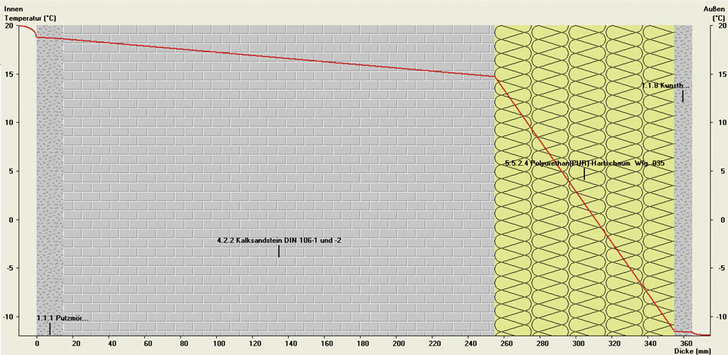
Die klassische Außenwand
Um das Gefühl für einen konkreten Wert zu bekommen sei eine klassische Außenwand gegeben mit folgenden Schichten, aufgezählt von innen nach außen:
Schicht 1:
1,5 cm Innenputz mit
λ-Wert von 0,87 W/(mK)
Schicht 2:
24 cm Kalksandstein mit
λ-Wert von 0,56 W/(mK)
Schicht 3:
10 cm Wärmedämmung mit
λ-Wert von 0,035 W/(mK)
Schicht 4:
1,0 cm Außenputz mit
λ-Wert von 0,70 W/(mK)
Die Werte werden gesammelt:
Rsi = 0,13 m²K/W (horizontal innen)
Rse = 0,04 m²K/W (extern, außen)
Für Schicht 1 gilt:
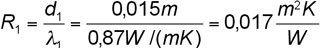
.
Für Schicht 2 gilt:
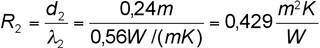
.
Für Schicht 3 gilt:
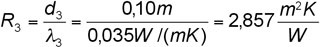
.
Für Schicht 4 gilt:
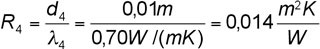
.
Die Addition der Widerstände ergibt den Gesamtwiderstand.
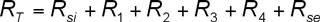
.
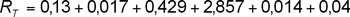
(die Einheit ist jeweils m²K/W)

.
Der Widerstand Wärme abzugeben beträgt also 3,487 m²K/W.
Der Kehrwert des Wärmedurchlasswiderstandes ergibt den U-Wert:

.
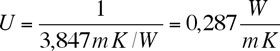
An dieser, schon recht gut isolierenden Außenwand, würden bei einer angenommenen Fläche von 10 Quadratmetern und einer Temperaturdifferenz zwischen drinnen und draußen von 30 Kelvin
0,287W/(m²K) · 10 m² · 30 K = 86 W
rund 86 Watt abgegeben.
.
Es ist schon durch bloßes Hinschauen relativ klar, dass Wärmedämmungen ein Gebäude gegen Auskühlung schützen. Schaut man sich die Formel zur Berechnung des U-Wertes an, wird schnell deutlich: Der größte Wärmedurchgangswiderstand – hier im Beispiel Schicht 3 mit 2,857 m²K/W – wird auch durch die Wärmedämmschicht erreicht. Alle Widerstände zusammen ergeben den Gesamtwiderstand und der Kehrwert ergibt den U-Wert.






