Widerstand in der Wand?

Der U-Wert – oder lang gesprochen der Wärmedurchlasskoeffizient – in der Einheit W/(m²K) ist für Architekten, Bauherren, Anlagenmechaniker und viele andere am Bau eines Hauses beteiligte Menschen eine wichtige Größe. Gibt doch dieser Wert Aufschluss über eine Leistung in Watt (W) bezogen auf eine Fläche in Quadratmeter (m²) sowie bezogen auf eine Temperaturdifferenz in Kelvin (K).

Konkretes Beispiel

Zur Erläuterung betrachten wir als Beispiel ein Fenster mit einer Breite und Höhe von jeweils 1 m. Damit beträgt die Fläche genau 1 m².
Dieses Fenster besitzt einen U-Wert von
1 W/(m²K).
In Worten kann man diesen Wert mit seiner Einheit
W/(m²K) folgendermaßen ausdrücken:
Ich gebe 1 Watt Leistung ab, wenn man 1 m² meiner Fläche betrachtet und nur 1 Kelvin Temperaturunterschied anliegt. Aber für 1 Kelvin Temperaturdifferenz baut keiner eine Heizung ins Haus.
Bei eisiger Kälte draußen, beispielsweise bei –10 °C, ist das allerdings etwas anderes. Drinnen möchte man angenehme 20 °C haben, um sich wohl zu fühlen. Nun stellt sich die Frage, welche Wärmeleistung genau dann an diesem Fenster abgeht.

An diesem Fenster würde eine Leistung abfließen von 30 Watt.
Man könnte jetzt beliebige andere Flächen, U-Werte oder Temperaturdifferenzen einsetzen und sicher voraussagen, welche Leistung an diesem Bauteil abfließen würde und folglich auch durch einen  Heizkörper oder eine Fußbodenheizung erbracht werden müsste.

Wie wird's berechnet?

Die Berechnung des U-Wertes ist nur auf den ersten Blick fremd. Hat man die Grundzüge verstanden, ist man in der Lage, zum Teil schon per Kopfrechnung Überschlagswerte auszuspucken.
Die Grundformel zur Entwicklung des U-Wertes lautet:

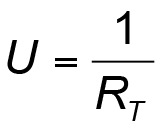
Der U-Wert ergibt sich also aus dem Kehrwert des Wärmedurchlasswiderstandes RT.
Aber wie errechnet sich dann RT? Für diesen Wert gilt folgende Gleichung:

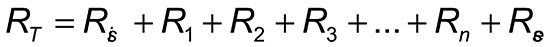
In Worten könnte man sagen: Addiere alle Einzelwiderstände zu einem Gesamtwiderstand (RT) auf. Die Einzelwiderstände setzen sich zusammen aus dem ersten (Rsi) und letzten (Rse) vom gleichen Typ sowie die „Schichtwiderstände“ 1 (R1) bis zur letzten (n-ten sprich Enten) Schicht (Rn). Die als Übergangswiderstände bezeichneten Rsi und Rse ergeben sich aus Tabellen.
Für Rsi, also den inneren Übergangswiderstand, sind nur drei Werte relevant. Je nach Wärmestrom ergeben diese sich wie folgt:

Für Rse also den externen (äußeren) Übergangs­widerstand gilt: Rse = 0,04 m²K/W

Es fehlen als letzte Größen also nur noch R1 bis Rn. Hierfür sieht es formell so aus:

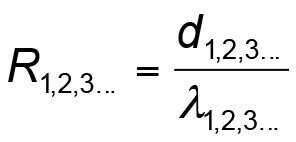
Das heißt: Dicke der betrachteten Schicht geteilt durch den Lambda-Wert dieser Schicht ergibt den Widerstand jeder einzelnen Schicht. Die Dicke der Schicht lässt sich ja noch ausmessen oder irgendwie bestimmen. Aber was hat es mit dem Lambda-Wert (λ-Wert) auf sich?
Der Lambda-Wert beschreibt die Wärmeleitfähigkeit eines Stoffes. Gute Wärmeleiter wie Kupfer haben einen Lambda-Wert von beispielsweise 380 W/(mK).
Das heißt in einer Autobiografie: Ich bin Kupfer und selbst wenn ich eine 1 m dicke Wand bin, so transportiere ich immer noch 370 Watt an Wärmeleistung, wenn drinnen 20 °C herrschen und draußen 19 °C.
Dem gegenüber hat eine gebräuchliche Isolierung wie Mineralwolle einen Wert von 0,035 W/(mK).
Auch hier die kurze Biografie: Ich bin Mineralwolle und wenn ich eine 1 m dicke Wand bin, so transportiere ich nur noch 0,035 Watt an Wärmeleistung, wenn drinnen 20 °C herrschen und draußen 19 °C.

Die klassische Außenwand

Um das Gefühl für einen konkreten Wert zu bekommen, ist hier eine klassische Außenwand gegeben mit folgenden Schichten, aufgezählt von innen nach außen:

An dieser schon recht gut isolierenden Außenwand würden bei einer angenommenen Fläche von 10 m2 und einer Temperaturdifferenz zwischen drinnen und draußen von 30 Kelvin

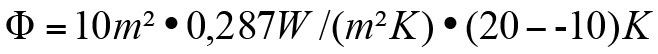
rund 86 Watt abgegeben.

Es ist schon durch bloßes Hinschauen relativ klar, dass Wärmedämmungen ein Gebäude gegen Auskühlung schützen. Schaut man sich die Formel zur Berechnung dieses U-Wertes an, wird schnell deutlich: Der größte Wärmedurchgangswiderstand – hier im Beispiel die dritte Schicht mit 2,857 m²K/W – wird durch die Wärmedämmschicht erreicht.
Der gesamte Aufbau ist 36,5 cm dick. Dabei beträgt die Dämmung 10 cm und damit rund 27 % der gesamten Dicke der Wand. Die Dämmung alleine macht aber 82 % des gesamten Widerstandes aus.
Alle Widerstände zusammen ergeben den Gesamtwiderstand und dessen Reziprok ergibt den U-Wert.

Bild: mihtiander / thinkstock

Was gibt's noch?

Dadurch, dass man den Rechenzauber eines U-Wertes entzaubert hat, versteht man auch viele andere Zusammenhänge, so beispielsweise diesen:
Die Reihenfolge eines Wandaufbaus kann für den U-Wert nur egal sein, denn an welcher Stelle die Addition stattfindet, spielt weder beim Addieren, noch beim endgültigen U-Wert eine Rolle.
Nicht so beim Temperaturverlauf. Bei absolut gleichen Schichten hängt der Verlauf der Temperatur erheblich von der jeweiligen Lage der Schicht ab.
Folgen Sie der nachstehenden Logik und verstehen Sie, was gemeint ist:
Der Gesamtwiderstand der Wand ist für die gesamte Temperaturdifferenz verantwortlich.
Im Beispiel ist es drinnen 20 °C warm und draußen –10 °C kalt. Dazwischen blockt der Gesamtwiderstand mit 3,487 m²K/W die beiden Temperaturen gegeneinander ab. Und jeder einzelne Widerstand trägt genau seinen prozentualen Beitrag dazu bei:
0,130/3,487 = 3,70 %
0,017/3,487 = 0,49 %
0,429/3,487 = 12,3 %
2,857/3,487 = 81,9 %
0,014/3,487 = 0,40 %
0,040/3,487 = 1,15 %

3,70 % von 30 K entspricht 1,12 K
0,49 % von 30 K entspricht 0,15 K
12,3 % von 30 K entspricht 3,69 K
81,9 % von 30 K entspricht 24,6 K
0,40 % von 30 K entspricht 0,12 K
1,15 % von 30 K entspricht 0,34 K
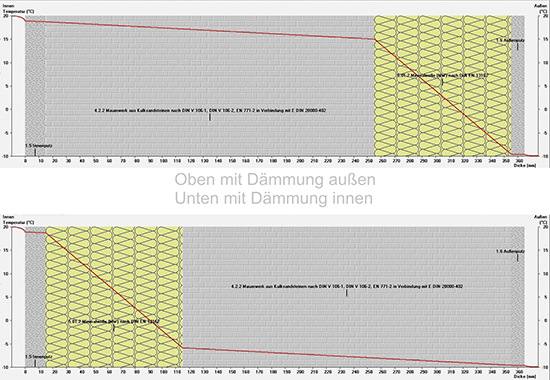
Das sind Rechenspielchen, könnte man denken. Fakt ist aber, dass die Dämmung außen, also wie im Beispiel berechnet, einen anderen Temperaturverlauf in der Wand zur Folge hat wie die gleiche Dämmung, jedoch innen eingesetzt.
Die zwei Grafiken zeigen dies anschaulich.
Und nun kann man raten, welcher Wandtyp innen mehr Speicherkapazität bietet bezüglich der Wärme? Genau, der Wandtyp mit der Außendämmung.
Beide Wände haben den gleichen U-Wert, verhalten sich aber unterschiedlich. So ist beispielsweise das Aufheizverhalten bei Außendämmung deutlich behäbiger. Tonnenweise Stein will zuerst erwärmt werden, da es innen auf der warmen Seite liegt. Dafür kühlt die Wand mit Außendämmung natürlich auch nur ganz behäbig ab, weil die aufgeheizte, warme Speichermasse sich nur sehr langsam entwärmen lässt. Selbst wenn man mal ein Fenster zum Lüften öffnet, bleibt die innenliegende, schwere Kalksandsteinwand warm.
Nicht so bei der Innendämmung. Da lässt sich ein Raum sehr flink aufheizen, hat aber kaum erwärmte Speichermasse zur Verfügung, denn die zum Raum gerichtete Wolle wiegt ja nicht viel. Ein solcher Raum kühlt bei offenem Fenster also schneller empfindlich ab.
Spinnt man die Situation weiter auf eine massive Wand nur aus Beton und einer Leichtbauwand nur aus Holz und Dämmung, so wäre der anschauliche Vergleich eines Bunkers mit einem Holzhaus geboren. Beide sollen den gleichen U-Wert besitzen, aber beide werden sich aufgrund der Speichermasse der Außenwände unterschiedlich verhalten. Solche Gedankenexperimente funktionieren übrigens gut mit solchen krassen Unterschieden. Damit kann man auch einem Laien bestens beschreiben, was Sache ist.

Bild: shkonst / thinkstock

Wirtschaftlichkeit von Dämmung

Seit Jahren werden bestehende Häuser in Deutschland nachträglich gedämmt. Dieser Trend sollte dafür sorgen, dass die Heizkosten in diesen frisch gedämmten Häusern sinken. Da stellt man sich schnell die Frage nach dem Nutzen von Dämmung oder, um auf das Thema des Berichts zurückzukommen, wie wirken sich die Anschaffungskosten einer Dämmung auf die zu erwartende Einsparung aus?
Dazu schauen wir uns eine Sanierungswand mit unterschiedlicher Dämmung an. In Schritten von jeweils 1 cm wird die Schichtdicke und damit der Aufwand zur Dämmung des Hauses erhöht.
Eine Außenwand mit Innenputz und 36,5er-Kalksandstein ist dabei die Ausgangsbasis.
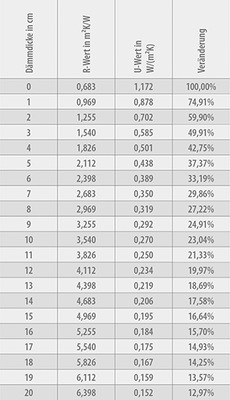
In der nachfolgenden Tabelle steht in der ersten Zeile diese Wand mit R- und U-Wert als Basis.
Wird dann 1 cm Dämmung aufgebracht, verändert sich der Wert beträchtlich, bei 2 cm ist die Veränderung immer noch riesig, aber nicht mehr so groß wie beim ersten Zentimeter.
Die Veränderung wird mit steigender Dämmschichtdicke immer geringer, betrachtet man den U-Wert und damit die Wärmeabgabe.
Vergleicht man, um die Erkenntnisse dieses Rechenbeispiels auf den berühmten Punkt zu bringen, die ersten 5 cm mit der nächsten Verdoppelung auf 10 cm, so stellt man fest, dass eine Verdoppelung von 5 auf 10c m nicht annähernd eine Verdoppelung der Dämmwirkung erbracht hat.

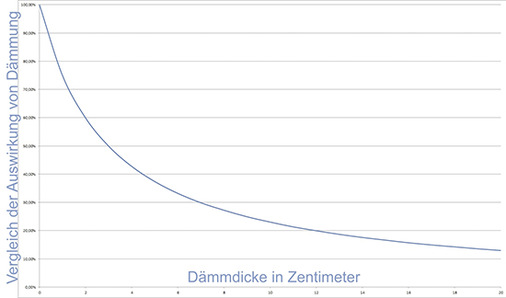
Grafisch lässt sich das auch noch mal anschaulich darstellen. Die Zunahme der Dämmstärke hat einen immer geringeren Effekt.
Die Logik des Alltags lässt sich also nicht auf die Logik eines ­U-Wertes übertragen.
Das Dämmen von Häusern oder auch von Rohrleitungen ist nämlich solchen Gesetzen der Physik unterworfen. Und damit einher geht immer auch der wirtschaftliche Aspekt, Aufwand und Nutzen gegeneinander abzuwägen. Es lohnen sich die ersten paar Zentimeter am meisten, leider.
Ein etwas verwirrter Anlagenmechaniker würde dann zu dem Schluss kommen: Okay, dann dämme ich statt einmal mit 12 cm lieber viermal mit 3 cm und kann diesen Effekt dann mehrfach nutzen. Träum weiter …

Bild: Suppofamily / thinkstock

Bild: zlikovec / thinkstock