Lufterwärmung im Mollier-Diagramm
.
Die Frage nach der Kompliziertheit stellt sich jedes Mal, wenn dieses Diagramm während eines Vortrages gezeigt wird. Das gilt für Berufsschulen und Hörsäle an Unis gleichermaßen. Dabei gibt es gute Gründe, es so einzusetzen wie es nun mal ist.
.

.
Die Veränderungen von Luft durch äußere Einflüsse sind äußerst vielfältig. Den Anlagenmechaniker interessieren in der Regel nur die thermodynamischen Einflüsse, sieht man mal von miefiger Luft in einem unbelüfteten WC ab. Und thermodynamische Prozesse bezeichnen eben die Änderungen bezogen auf den Energiegehalt von Luft.
Etwas Alltägliches
Aus dem Alltag ist bereits bekannt, dass man Luft erhitzen und abkühlen kann. Nichts Besonderes und beim alltäglichen Wasser nichts anderes. Luft ändert aber auch laufend ihre Zusammensetzung. Insbesondere der Feuchtegehalt von Luft ist von Interesse. Die extrem heißen Tage des bisherigen Sommers führten schweißtreibend vor, was es bedeutet, nicht nur warme, sondern sogar schwül-warme Luft aushalten zu müssen. Umgangssprachlich ist die Luft nun mal heiß oder kalt oder feucht oder trocken. Beim Wasser ist das ein wenig anders. Zum Wasser gibt es zum einen natürlich auch Diagramme, aber dieses h-x-Diagramm, wie es für feuchte Luft existiert, wäre für Wasser nicht notwendig. Beim Wasser unterscheiden wir als thermodynamisch relevante Größe auch heiß und kalt, aber natürlich nicht feucht oder trocken. Die Bestandteile und Inhaltsstoffe von Wasser sind in der Regel weit weniger interessant als die von Luft. Sollten mal ein paar Luftmoleküle mehr im Wasser eingeschlossen sein als gewöhnlich, wirft das nicht gerade eine Heizungsanlage aus der rechnerischen Bahn. Umgekehrt ist das schon anders. Luft verändert den Energiegehalt auch in Abhängigkeit von der Feuchte. Also, das Mollier-Diagramm für Luft ist eine hilfreiche Einrichtung um Zustände von Luft zu beschreiben. Nachfolgend mal ein paar Ansätze.
.
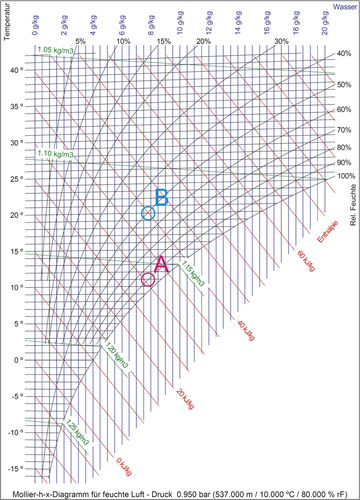
.
Zwei Ablesebeispiele
Punkt A in Bild 2:
.
- Temperatur in Grad Celsius: 11
- Relative Luftfeuchte in Prozent: 90
- Absolute Luftfeuchte in Gramm pro Kilogramm trockener Luft: 7,8
- Dichte in Kilogramm pro Kubikmeter: 1,16
- Spezifische Enthalpie in Kilojoule pro Kilogramm: 31
.
Anmerkungen und Erläuterungen zu diesen Ablesungen:
Die Temperatur ist noch das harmloseste zur Ablesung und wird wie auch sonst in Grad Celsius angegeben.
Die relative Luftfeuchte hingegen ist, wie der Name schon sagt „relativ“. Und zwar immer relativ zum Maximum bei der jeweiligen Temperatur. Könnte die Luft beispielsweise 10 Gramm an Feuchtigkeit aufnehmen, hätte aber nur 5 Gramm aufgenommen, dann wären das 50 Prozent - oder eben die Hälfte dessen was überhaupt ginge.
Die absolute Feuchte, wen wundert es, ist absolut. Also wie viel Gramm an Feuchte oder anders gesagt dampfförmigen Wasserdampf enthält die Luft?
Die Dichte wiederum ist eine recht gebräuchliche Größe. Hier gibt die Dichte an, wie viel Kilogramm ein Würfel aus Luft mit der Kantenlänge von einem Meter wiegt.
Die spezifische Enthalpie, auch gerne nur Enthalpie genannt, bezeichnet den Energiegehalt der Luft. Es fällt beim genauen Hinsehen auf, dass die Enthalpie nicht alleine von der Temperatur abhängt. Luft von 18 °C kann durchaus eine höhere Enthalpie besitzen als Luft von 20 °C.
.
Punkt B in Bild 2:
.
- Temperatur: 20 °C
- Rel. Luftfeuchte: 50 %
- Abs. Luftfeuchte: 7,8 g/kg
- Dichte: 1,125 kg/m³
- Enthalpie: 40 kJ/kg
.
Eine Aufgabe
Folgende Aufgabenstellung beschäftigt sich mit den soeben beschriebenen Ablesebeispielen.
.
Es sollen 100 m³ Luft von 11 °C mit einer Luftfeuchtigkeit von 90 % auf 20 °C erwärmt werden. Welche Energiemenge und welche Leistung werden dazu notwendig sein um diese Masse innerhalb einer Stunde zu erwärmen?
.
Aus dem Ablesebeispiel ist bereits die Ausgangssituation bekannt und in Punkt A (Bild 2) ablesbar. Es wird schnell klar, wenn ein Kubikmeter 1,16 Kilogramm wiegt, dann werden 100 Kubikmeter wohl das 100-fache wiegen. Wenn also jemand 100 Kubikmeter der beschriebenen Luft bewegt, dann sind das 116 Kilogramm. Der Energiegehalt eines Kilogramms dieser beschriebenen Luft beträgt 31 Kilojoule, also enthalten 116 Kilogramm 3596 kJ an Energie.
.

.
Zur Erwärmung benötigt man die Daten der erwärmten Luft, die bereits beim Ablesebeispiel „B“ (Bild 2) zusammengetragen wurden. Wie aber kommt man zu der Logik, dass nach der Erwärmung der Kaltluft von 11 °C und 90 % relative Feuchte die Erwärmung in Richtung Ablesebeispiel „B“, also senkrecht verläuft? Hier erschließt sich eines der „Geheimnisse“ des Mollier-Diagramms. Wenn keiner was weg nimmt oder hinzu gibt, außer Wärme, dann verläuft dieser Prozess einfach senkrecht im Mollier-Diagramm, denn es ändert sich ja „nur“ die Temperatur.
Also der Punkt B ergibt eine Enthalpie von 40 kJ/kg. In 116 Kilogramm Luft, die man durch den Lufterhitzer gejagt hat, sind also am Ende 4640 kJ enthalten. Das bedeutet, um die Luft aus der Ausgangssituation entsprechend der Vorgabe zu erwärmen, musste die Enthalpie von ursprünglich 3596 kJ auf 4640 kJ angehoben werden. Der Lufterhitzer hatte also 1044 kJ an Wärmeenergie hinzuzufügen. Über die Leistung des Lufterhitzers ist an dieser Stelle noch nichts gesagt. Er könnte ja mit sehr hoher Leistung diese 100 m³ sehr schnell erwärmen oder eben bei geringer Leistung die Luft nur allmählich auf Temperatur bringen. Laut Aufgabe soll der Vorgang innerhalb einer Stunde ablaufen. Eine Stunde entspricht 3600 Sekunden. Für die Berechnung der Leistung teilt man nur noch die Energie, welche bereits in Joule angegeben ist, durch die Zeit in Sekunden und erhält Watt. Man erinnere sich kurz: Joule pro Sekunde ist Watt. Daher gilt für die Beispielaufgabe: 1044 Kilojoule geteilt durch 3600 Sekunden gleich 0,290 Kilowatt. Der Lufterhitzer benötigt also für die gestellte Aufgabe eine Leistung von 0,290 kW oder 290 Watt.
.

.
Was ist noch passiert?
Während der Erwärmung hat sich die Luft ausgedehnt. Die Dichte ist von 1,16 kg/m³ auf 1,125 kg/m³ abgesunken. Aus den ehemals angesaugten 100 Kubikmetern an Luft wurden so 103 Kubikmeter. Und was deutlich gravierender wirkt, ist die Abnahme der relativen Feuchte. War die relative Feuchte bei 11 °C bereits annähernd gesättigt bei fetten 90 %, reduziert sie sich durch die Erwärmung auf 50 %. Der Grund ist in der Aufnahmefähigkeit der Luft für Feuchte zu sehen. Je höher die Lufttemperatur steigt, desto mehr Feuchte lässt sich darin unterbringen. Bei 11 °C, also vor der Erwärmung, konnte die Luft maximal lediglich 8,7 Gramm Feuchte aufnehmen, ablesbar an der 100 % Linie. 7,8 Gramm an tatsächlicher Feuchte geteilt durch 8,7 Gramm an maximaler Feuchte machten die bereits abgelesenen 90 % relativer Feuchte aus. Wenn, wie in dieser Aufgabe gefordert, die Luft nur erwärmt wird, also niemand Feuchte hinzufügt oder entfernt, dann ist auch nach der Erwärmung auf 20 °C noch 7,8 Gramm Feuchte enthalten. Aber diese erwärmte Luft könnte deutlich mehr Feuchte aufnehmen, nämlich ca. 15,6 g/kg, laut der 100 %-Linie ganz rechts. Folgt man der senkrechten Linie für die absolute Feuchte nach unten, stößt man unweigerlich nochmals an die 100 %-Linie. Luft von minus 9 °C kann ca. 7,8 g/kg an Feuchte aufnehmen. Würde die Temperatur für diese Luft unter minus 9 °C gesenkt, so würde die Feuchte kondensieren.
.
Beispielsweise eine kalte Glasscheibe oder ein kühles Bierglas könnte diesen Effekt herbeizaubern. So würde man nebenbei Luft entfeuchten und den Prozess im h-x-Diagramm darstellen. Ab jetzt werden sie übrigens sehr lange und nachhaltig bei einem kühlen Glas Bier an das verflixte h-x-Diagramm denken, Prost.






