Mischwasserberechnung
.
Schlüsselerlebnisse sind jene herausragenden Momente im Leben, in denen sich plötzlich ein Tor aufstoßen lässt, das bisher verschlossen war.
.
.
Mathe-Freaks unter den Lesern können diesen Text jetzt getrost überfliegen und danach ein weiteres Integral zum Thema entwerfen oder lösen. Allen anderen sei versichert, dass es nicht zwingend langweilig ist sich mit Fachmathe zu beschäftigen. Quälend wird es leider nur, wenn abstrakte Formeln und Zahlen ein, wie auch immer geartetes Interesse verhindern. Spannend wird es oft erst, wenn Alltägliches sich nicht nur über die Erfahrung, sondern auch mathematisch erschließen lässt. Als Beispiel sei hier einmal die Mischwasserberechnung angeführt.
.
Erfahrungen hervorkramen
Schon ab der Zeit, wo wir uns selbst das Badewasser einlassen durften, wissen wir aus eigenem Erleben, wie wir das Mischen anstellen sollen. Etwas mehr von dem Kalten und die Mischung in der Wanne ist entsprechend niedriger temperiert. Zum Schluss vielleicht noch etwas Heißes und die Temperatur erfährt einen Kick nach oben. Bereits ein Grundschulkind kann, bewaffnet mit einem Thermometer, eine Wannenfüllung auf eine vorgegebene Temperatur bringen, so viel ist wohl anzunehmen. Eine mathematische Formel hat es dabei nicht zwingend im Kopf. Lediglich die Vorstellung und Erfahrung reichen aus, um diese Aufgabe zu lösen. Mit Trial and Error, also Versuch und Irrtum, wird nach mehrmaligem Wiederholen, eine angestrebte Temperatur in immer kürzerer Zeit von dem Kind in die Wanne eingelassen werden können. Und nun zur eigentlichen Formel.
.
Formelkunde
Im folgenden Text wird der Sachverhalt, der dem Schulkind bereits geläufig ist, in eine mathematische Formel gegossen. Es soll dabei bereits bekannt sein, dass ein Liter Wasser rund ein Kilogramm an Gewicht hat.
Man nehme zuerst („römisch Eins“, also I) eine gewisse Menge Wasser mit einer gewissen Temperatur
Gesprochen:
Formel:
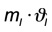
und eine zweite Menge Wasser (II) mit einer anderen Temperatur (II).
Gesprochen:
Formel:
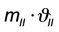
Man gießt diese beiden Mengen zusammen
Formel:
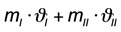
und erhält Mischwasser mit einer gewissen Mischtemperatur.
Formel:
Die soeben entwickelte Formel stellt also letztlich die Erfahrungen dar, die beim Einlassen des Badewassers bereits ein siebenjähriges Kind machen kann. Damit ist natürlich nicht bewiesen, dass es auch die zugehörige Formel entwerfen könnte.
Plausibilität
Kann das richtig sein? So kritisch sollte man natürlich rangehen, wenn man eine solche Formel aus dem Hut zaubert. Zur Beweisführung bietet sich ein übersichtlicher Test an:
Ein Liter kaltes Wasser von 10 °C soll mit fünf Liter warmen Wassers von 40 °C zusammengeschüttet werden. Vor dem geistigen Prüfstand sieht man den Messbecher mit nur einem Liter und den mittleren Eimer mit fünf Litern.
Erste Prognosen ergeben, dass die Temperatur der Mischung deutlich näher an 40 °C liegen wird als an 10 °C. Ist logisch, denn der Einfluss der größeren Masse ist selbstverständlich höher.
Fein säuberlich zusammengestellt gilt als gegeben:
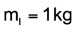
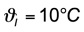
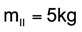
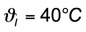
Zur Umstellung der Formel ist mathematisches Handwerkszeug erforderlich, schon klar, aber das ist ja auch kein Hexenwerk. Gesucht ist die Mischtemperatur. Gefasst in Formeln und Kürzel ergibt sich:
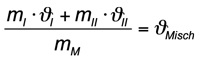
Und nach Einsetzen der bereits bekannten Werte steht da:

Mit Schrecken würde der Laie jetzt kurzerhand aufgeben, entdeckt er doch eine Gleichung mit zwei Unbekannten. Das 7-jährige Schulkind würde diesen Laien jedoch zurückpfeifen an den Versuchstisch, denn es erkennt sofort, dass die Masse des Mischwassers sich aus der Addition der beiden Massen I und II ergibt.
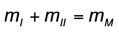
Letztlich steht dann die Formel da mit:
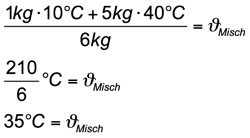
Die Mischtemperatur beträgt also 35 Grad Celsius und ist damit deutlich näher an 40, als an 10 Grad Celsius wie bereits prognostiziert. Der praktische Versuch wird diesen Test untermauern.
.
.
Umsetzbare Logik
An diesem recht flachen Beispiel der Mischwasserrechnung wird deutlich, mit welchen Problemchen wir uns herumschlagen müssen. Und die Lösung fällt, wenn man ehrlich ist, doch nicht so schwer. Schaut man sich ein anderes klassisches Problem der SHK-Branche an, erkennt man wie gut dieses Prinzip auch in anderen Fällen funktioniert. Das Beispiel zur Bestimmung der Leistung einer Pumpe ist hier sehr anschaulich. Die Pumpe fördert ein Volumen und erhöht den Druck. Je mehr Volumen die Pumpe fördert oder je mehr der Druck erhöht wird, umso mehr leistet sie. Die Formel lautet daher:
Leistung = Volumenstrom mal Druckdifferenz
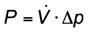
Eigentlich und uneigentlich logisch, oder?
Während es uns Flachlandmathematikern noch möglich ist die geschilderten Zusammenhänge zu erkennen, versagen bei den meisten von uns aber die tiefen Erkenntnisse warum denn wohl
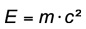
sein soll. Aber spinnen sie es doch mal durch! Und? Hatten sie jetzt ein Schlüsselerlebnis? Wenn ja, lassen sie es uns wissen, gerne auch anonym.






