Man erkennt die Grundlagen der Strömungstechnik beispielsweise beim Ablassen des Wassers aus einem Trinkwassererwärmer, umgangssprachlich auch Boiler genannt. Gehen wir davon aus, dass an einer Entleerung ein Schlauch angeschlossen wurde und dieser das Wasser zum nächsten Bodenablauf befördert. Anfangs, also bei vollem Druck, schießt es raus aus dem Schlauch. Die Fließgeschwindigkeit nimmt während des Leerlaufens stetig ab. Zum Ende tröpfelt es nur noch. Diese Erfahrung beschreibt bereits den Zusammenhang zwischen Druckdifferenz und Fließgeschwindigkeit, um den es in diesem Bericht geht.
Weitere Erfahrungswerte
Wird der Entleerungshahn am Boiler nur minimal geöffnet, tritt weit weniger Wasser pro Zeiteinheit aus als bei voller Öffnung. Die Strömung hängt also auch vom Widerstand ab, der dem Druck entgegensteht. Eine kleine Öffnung stellt einen großen Widerstand dar und mit zunehmendem Öffnungsquerschnitt nimmt dieser Widerstand ab. Das Füllen eines Wassereimers klappt ja auch erfahrungsgemäß am schnellsten, bei einem voll geöffneten Hahn. Beobachtungen dieser Art führten die Physiker zur Entwicklung von Formeln über das Fließen von Fluiden, also Gasen und Flüssigkeiten. Daniel Bernoulli brachte es im 17. Jahrhundert auf den Punkt. Eine wichtige Formel der Strömungstechnik ergab sich schließlich aus diesen Betrachtungen und wird Bernoulli-Gleichung genannt.
Zusammenhänge
In der Strömungstechnik gilt, dass sich eine Druckdifferenz in einer Rohrleitung durch folgenden Zusammenhang ergibt:
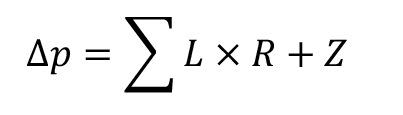

(Deltapgleichsummeauselmalerpluszett)
dabei bedeutet
Δρ= Druckdifferenz
∑ = mathematisches Zeichen „Summe aus“
L = Länge des Rohres
R = Rohrreibungsdruckgefälle
Z = Druckverl. in Einzelwiderständen
Im folgenden Text soll gedanklich Wasser durch ein Rohr fließen. Die Ausführungen sind dann übertragbar auf andere Fluide wie Gase.
– L – Die Länge macht's
Klar ist, dass das Wasser sich an den Rohrwandungen reibt. Die Moleküle stoßen an die raue Oberfläche und stolpern in die Vertiefungen und werden im nächsten Moment wieder von anderen Molekülen mitgerissen. Sichtbar wäre die beschriebene Rauigkeit mit dem bloßen Auge sicherlich nicht. Aber so ein H2O-Molekül ist eben winzig klein und rumpelt über diese Vertiefungen. Und je weiter der Weg über diese Buckelpiste verläuft, je länger die durchströmte Rohrstrecke ist, desto stärker werden die Moleküle ausgebremst. Die Länge des Rohres vergrößert also die Druckdifferenz.

– R – Rohrreibungsdruckgefälle
Das soeben beschriebene Rumpeln der Moleküle durch das Rohr findet auf einer für das bloße Auge als glatt wahrgenommenen Oberfläche statt. Die fast spiegelblanke Innenoberfläche eines Rohres aus Polyethylen oder Kupfer verspricht eine Autobahn der besten Güteklasse. Aber es liegt eben an den Größenrelationen, wann etwas als rau betrachtet wird. Ein Muldenkipper, wie im Bild dargestellt, mit seinen riesigen Rädern, wird bei voller Fahrt ein fünfzig Zentimeter tiefes Schlagloch kaum registrieren, während es einem durchfahrenden PKW die Achse wegdonnert. Und ein winziges Wassermolekül verschwindet schon mal in den mikroskopisch kleinen Tälern einer Rohrinnenoberfläche. Die Hersteller von Rohren sorgen natürlich einerseits für eine glatte Innenoberfläche, soweit dies fertigungstechnisch sinnvoll und möglich erscheint. Und es werden entsprechende Tests durchgeführt, in denen das Strömen von Fluids erprobt wird. Dabei ergeben sich dann charakteristische Werte für die Rauigkeit eines Rohres. Diese Rauigkeit lässt sich dann rechnerisch auf einen Druckverlust pro laufenden Meter umrechnen. Es gibt aber nicht einen Wert für ein bestimmtes Rohr, sondern im Prinzip unendlich viele. Denn der Druckverlust hängt von dem jeweiligen Volumenstrom im Rohr ab. Je mehr Wassermoleküle durch das Rohr geprügelt werden, umso derber werden diese an die Wandungen gedrückt und reiben sich entsprechend heftig. Daher werden in Tabellen oder Diagrammen die Werte einem jeweiligen Volumenstrom zugeordnet. Der kleine Auszug einer solchen Tabelle zeigt ein Ablesebeispiel.

– Z – Einzelwiderstände
Werden die Wasserteilchen zu einer plötzlichen Richtungsänderung gezwungen, so kostet dies Energie. Eine einmal angestoßene Billardkugel ändert ja auch nicht ohne äußeren Einfluss die Richtung. Neben der einfachen Reibung verursachen Richtungsänderungen also nochmals einen Druckverlust. Wird diese Änderung von einem sehr langsamen Wasserteilchen vollzogen, so schmiegt es sich vielleicht noch an die äußere Wandung des Bogens. Soll dieser Bogen aber mit hoher Geschwindigkeit durchlaufen werden, kommt es gewissermaßen zu Überschlägen und anderen Kapriolen. Die Geschwindigkeit, mit der das Wasser also eine Richtungsänderung vollzieht, spielt eine große Rolle. Auch ist entscheidend, wie strömungsgünstig beispielweise ein Bogen geformt ist. Lang gestreckt läuft besser als in einer engen Kehre. Und so hat man den Bauteilen, die üblicherweise in einem Rohrverlauf auftauchen, den Wert eines Einzelwiderstandes zugeordnet, den so genannten Zeta-Wert. Der eigentliche Druckverlust eines Einzelwiderstandes ergibt sich dann aus:
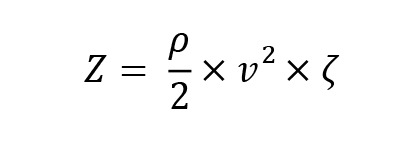
 ρ = die Dichte des Fluids
(griech. Buchst., gesprochen: Rho)
v = die Geschwindigkeit des Fluids
 ζ = der Widerstandsbeiwert
(griech. Buchst., gesprochen: Zeta)
Versuch macht klug
Ein Kupferrohr DN 20 soll auf einer Länge von 10 Metern einen Volumenstrom von 0,5 Litern pro Sekunde transportieren. Auf dieser Strecke ist ein Bogen DN 20 montiert, mit einem Widerstandsbeiwert von 0,7. Wie hoch ist der Druckverlust der gesamten Leitung?
Bereits bekannte Werte sind:
L = 10 m
 ρ für Wasser = 1000 kg/m³
 ζ für einen Bogen = 0,7
Und aus der zugehörigen Tabelle für Kupferrohr kann man ablesen:
R = 15,7 mbar (1570 Pa/m) bei einer Geschwindigkeit „v“ von 1,6 m/s.

Die Nachbarwerte in der dargestellten Druckverlusttabelle zeigen: Das nächste kleinere Rohr, also DN 15, hätte einen deutlich höheren Druckverlust (45,7 mbar) hervorgerufen und DN 25 einen entsprechend deutlich geringeren (5,4 mbar).
In die Formel für Einzelwiderstände eingesetzt ergibt sich dann für einen Bogen:


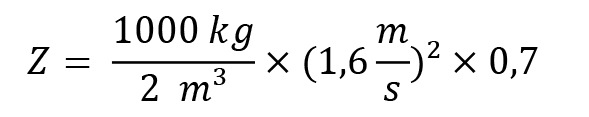


Die Summe der Druckverluste beträgt dann:
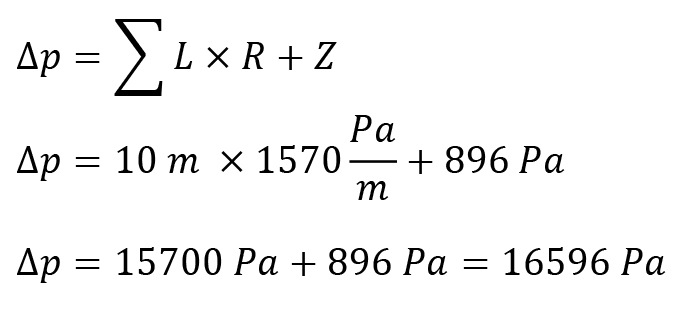
Diese Rohrstrecke mit Bogen stellt also einen Widerstand von 16 596 Pa oder rund 166 mbar dar.
Weitere Schlauheiten?
Anfangs wurde bereits erwähnt, dass diese Formel (eine der „ewigen Wahrheiten“ wie auch Kuhistgleichemmalcemaldeltatheta) für Fluide allgemein gilt. Und klar ist natürlich, dass man eine dickflüssige Pampe schwieriger durch ein Rohr bewegen kann als das dünnflüssige Wasser aus dem Beispiel. Auch ein Gas gehorcht der Bernoulli-Gleichung. Der Berechnung liegen dann aber angepasste Druckverlusttabellen zugrunde. Ein weiterer Schluss, der aus den vorgenannten Ausführungen gezogen werden kann, gilt sicherlich noch für die Bewegungen in einem Trinkwasserrohrnetz, die durch vorgegebene Druckdifferenzen hervorgerufen werden. Beispielsweise ein Strömungsteiler, wie die Sanitärindustrie ihn anbietet, sorgt ja bei einer Durchströmung für eine Druckdifferenz. Diese soll genutzt werden, um eine hygienische Durchspülung einer Rohrleitung zu ermöglichen. Eine Ringleitung mit entsprechenden Bögen und anderen Widerständen wird dabei durchflossen. Die mögliche Strömungsgeschwindigkeit lässt sich dann ebenfalls mittels Bernoulli-Gleichung errechnen: ein wichtiges Hilfsmittel auf dem Weg zu hygienischen Trinkwassersystemen. Im schnelllebigen Alltag greift man natürlich auf entsprechende Software zurück, um „old Bernoulli“ zu berechnen. Aber die Grundkenntnisse dieser Zusammenhänge sind sehr hilfreich beim Treffen von Entscheidungen im Umfeld der Trinkwasserhygiene, Gasversorgung und Heizungstechnik.
Dictionary
Entleerungsventil = discharge valve
Wasserschlauch = water hose
Druckverlust = loss of pressure
Rauigkeit = roughness







