Schwimmende Tanks
Der ein Kubikmeter große Granitblock erfährt im Wasser den gleichen Auftrieb wie ein ebenso großer Styroporwürfel. Bei dieser Tatsache fragt man sich, warum das Styropor an die Wasseroberfläche steigt, während der Stein bis auf den Behälterboden sinkt.

Und wieso schwimmt ein schwerer Heizöltank aus Stahl, während ein leichter Schraubendreher bei Unachtsamkeit unwiederbringlich in der Klärgrube versinkt?
Die Gewichtskraft
Als Gewichtskraft wird die Kraft bezeichnet, die ein Schwerefeld auf einen Körper bewirkt und diesen nach unten zieht. Die Physik hat festgelegt, dass die Gewichtskraft das Produkt aus der Masse eines Körpers und der jeweiligen Beschleunigung ist. Somit gilt beispielsweise auf der Erde:
Fg= m•g
Fg = Gewichtskraft
m = Masse
g = Erdbeschleunigung (9,81m/s²)
Um die Masse eines Granitblockes zu bestimmen, muss zuerst dessen Dichte ermittelt werden. Die Dichte liegt bei 2800 kg/m³.
Mit der Formel:
m = V • ρ
m = Masse in kg
ρ (Roh) =Dichte in kg/m³
V = Volumen in m³
lässt sich danach einfach die Masse berechnen.
m = 1 m³ • 2800 kg/m³
=> m = 2800 kg
Für den Granitblock mit einer Masse von 2800 kg bedeutet das eine Gewichtskraft von:
Fg= m • g
=> Fg = 2800 kg • 9,81 m/s²
=> Fg = 27500 kg •m/s²
=> Fg = 27500 N
Die Auftriebskraft
Auf jeden Körper in einer Flüssigkeit wirkt eine Auftriebskraft. Dabei ist es egal, ob dieser Körper an der Oberfläche schwimmt, auf einer bestimmten Tiefe schwebt oder zum Grund sinkt. Die Auftriebskraft entsteht durch den Schweredruck der Flüssigkeit. Mit größerer Tiefe steigt der Druck durch der sich über dem Körper befindlichen Wassersäule. Das kann jeder im Schwimmbad selbst ausprobieren. Das unangenehme Gefühl in den Ohren wird von dem Gewicht des Wassers erzeugt, das sich über einem befindet und auf das Trommelfell drückt. In Flüssigkeit breitet sich die Kraft bekanntlich in alle Richtungen gleich stark aus. Wenn man sich jetzt den Würfel vorstellt wird deutlich, dass der Druck und damit die Kraft des Wassers der auf die Unterseite wirkt durch die größere Tiefe höher ist als der Druck der auf den Oberseite wirkt. Dieser Kräfteunterschied wird als Auftriebskraft bezeichnet. Als Formel ausgedrückt folgt daraus:
Fa = F2 – F1
Fa = Auftriebskraft
F1 = Die Kraft auf den Deckel
F2 = Die Kraft auf den Boden
Die Kräfte F1 und F2 setzten sich jeweils zusammen aus der Fläche A1/A2 und dem darauf wirkenden Drücken p1/p2. Die Drücke wiederum sind abhängig von der Dichte der Flüssigkeit (ρ), der Erdbeschleunigung (g) und der Tiefe (h). Dann gilt:
p1 = A1 • ρFL • g • h1
p1 = Der Druck auf den Deckel
ρFl = Die Dichte der Flüssigkeit
g = Erdbeschleunigung
h1 = Eintauchtiefe
Das Gleiche gilt natürlich auch für die Kraft F2 , die auf den Boden wirkt. In unserem Beispiel sind die Flächen A1 und A2 gleich groß.
A = A1 = A2
Auch kann an Stelle der Differenz der Eintauchtiefen aus h2 und h1 die Höhe des Würfels angenommen werden. Da das Produkt aus Fläche und Höhe eines Würfels sein Volumen ist kann die Auftriebskraft auch kürzer mit:
Fa = A • h • ρFl • g
=> Fa = V • ρFl • g
Für den beschriebenen Granitblock bedeutet das im Wasser eine Auftriebskraft von:
Fa = VK • ρFl • g
=> Fa = 1 m³ • 1000 kg/m³ • 9,81 m/s²
=> Fa = 9810 N
Wenn man die Formel für die Berechnung der Gewichtskraft neben der Verwandten für die Auftriebskraft stellt erkennt man sofort die Ähnlichkeit. Wie zweieiige Zwillinge gibt der eine die Gewichtskraft des Körpers, der andere die Gewichtskraft der durch den Körper verdrängten Flüssigkeit wieder. Daraus lässt sich ableiten, dass die Auftriebskraft der Gewichtskraft der verdrängten Flüssigkeit entspricht. Um eine Aussage darüber treffen zu können ob ein Körper schwimmt, schwebt oder zu Boden sinkt muss man schließlich noch die Tauchgewichtskraft betrachten.

Die Tauchgewichtskraft
Die Tauchgewichtskraft ist die Differenz aus Gewichtskraft eines Körpers und seiner Auftriebskraft.
FT = Fg - Fa
FT = Tauchgewichtskraft
Fg = Gewichtskraft
Fa = Auftriebskraft
Ist das Ergebnis, also die Tauchgewichtskraft positiv, sinkt der Körper. Ist das Ergebnis = 0 schwebt er, und bei einer negativen Tauchgewichtskraft steigt er an die Oberfläche. Unser Stein mit einer Gewichtskraft von 27500 N und einer Auftriebskraft von 9810N hat also eine Tauchgewichtskraft von 17700N und sinkt damit zu Boden. Jedoch müsst man, um den Stein unter Wasser zu bewegen nur noch so viel Kraft aufbringen wie für einen rund 1800 Kg schweren Block über Wasser nötig wäre, weil einem der Rest vom Auftrieb abgenommen wird. Den versunkenen Goldschatz würde man also durchaus vom Meeresboden anheben können. Beim reinhieven ins Boot könnte es dann immer noch scheitern, weil dann die Unterstützung durch das Wasser fehlt.
Ein Gesetz des Archimedes lautet: Ein in einer Flüssigkeit schwimmender Körper sinkt so tief ein, dass die Gewichtskräfte des Körpers und der verdrängten Flüssigkeit gleich groß sind.
Jener ein Kubikmeter großer Styroporklotz mit einer Dichte von 60 kg/m³ sinkt folglich genau wie der Granitblock ins Wasser ein, auch wenn es vielleicht so aussieht als ob es nur die Oberfläche berühre. Wie tief lässt sich leicht errechnen:
Fg = VK • ρK • g
=> Fa = 1 m³ • 60 kg/m³ • 9,81 m/s²
=> Fa = 589 N
Fg = VK • ρFL • g
=> Fa = 1 m³ • 1000 kg/m³ • 9,81 m/s²
=> Fa = 9810 N
FT = Fg - Fa
=> FT = 589 N – 9810 N
=> FT = -9221 N
Die Tauchgewichtskraft ist negativ. das bedeutet, dass der Styroporwürfel schwimmt. Bei einer Gewichtskraft von 589 N und einer Grundfläche von 1 m² müsste der Würfel laut Archimedes 6 cm einsinken.
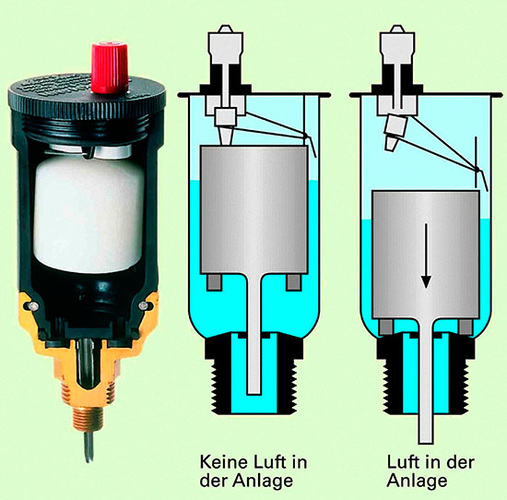
Praktische Anwendung
Jeder Installateur oder Heizungsbauer kennt die praktische Anwendung der vorhergegangenen Gesetzmäßigkeiten zum Beispiel aus dem Spülkasten, wo ein Styroporschwimmer das Füllventil schließt, wenn der Kasten gefüllt ist. Ein weiterer Anwendungsfall ist der Schnellentlüfter, in Fachcomics auch Snüffelstück genannt, der mit Hilfe einer Schwimmers dieses Ventil schließt sobald das Heizungswasser das Bauteil gefüllt hat. Dieser Schwimmer öffnet das Snüffelstück, wenn sich wieder Luft angesammelt hat. Es gibt jedoch auch Bereiche in der Installationstechnik wo der Auftrieb unerwünscht ist. Hier sind insbesondere erdgedeckte Tanks für Heizöl, Gas oder Zisternen zu nennen. Diese müssen entsprechend der möglichen Auftriebskraft in Gebieten mit hohem Grundwasserspiegel gegen ein Auftreiben verankert werden. Sonst verwandelt sich der erdgedeckte Tank nach einer langen Regenphase unter Umständen in einen halb oberirdischen. Dass es sich dabei nicht um ein kleines Ärgernis handelt wird deutlich, wenn man bedenkt, dass aus einem beschädigten Tank und abgerissenen Anschlussleitungen viele hundert Liter Öl oder Gas austreten können. Große Mengen Erdreich und Grundwasser drohen bei solch einem Ölleck zu verschmutzen und bei einem Gastank besteht erhöhte Explosionsgefahr.

Volumenvergrößerung
Es stellt sich natürlich die Frage, wieso der Heizöltank schwimmen kann, während der sehr viel leichtere Schraubendreher einfach versinkt. Der Trick besteht darin, dass Volumen im Verhältnis zur Gewichtskraft zu vergrößern. Um bei einem Behälter die Gewichtskraft zu berechnen, muss berücksichtigt werden, dass dieser innen hohl ist. Man darf in solch einem Fall nur das Volumen zur Massenbestimmung berücksichtigen, welches nach dem Einschmelzen oder der Schrottpresse übrig bleibt. Zur Berechnung der Auftriebskraft ist aber im Gegensatz dazu der das tatsächliche Volumen maßgeblich. Dieser Tatsachen machen sich auch Schiffkonstrukteure zu nutze. Durch die schalenförmige Bauweise steht dem Stahlklotz trotz seiner unglaublich großen Masse ein wesentlich größeres Volumen an verdrängtem Wasser gegenüber. Die Auftriebskraft ist also größer als die Gewichtskraft, und man kann mit trockenen Füßen an Deck stehen, während unter einem nichts als Wasser ist. Bei großen Frachtschiffen kann die Auftriebskraft sogar so groß werden, dass diese nach dem Löschen der Fracht ihre Ballasttanks fluten müssen, um nicht wie eine Nussschale auf den Wellen zu schaukeln und Gefahr laufen zu kentern.






