Mischungskreuz
Wassermassen von unterschiedlicher Temperatur zu mischen läuft selbst für den Anlagenmechaniker meistens im Hintergrund ab. Die Zusammenhänge lassen sich aber sehr gut darstellen und bringen wichtige Erkenntnisse fürs Arbeitsleben.

Und das ist, wie immer, Grund genug dieses Thema im SBZ Monteur darzustellen. Dabei schauen wir diesmal auf einen Lösungsansatz mittels der oft ungeliebten Formel und zusätzlich auf einen grafisch unterstützten Lösungsweg, nämlich des Mischungskreuzes.
Fragen aus der Praxis
Zwei Praxisbeispiele sollen den Bezug zum echten Leben herstellen.
Beispiel 1:
In einem Einfamilienhaus wird der bestehende Speicher von 150 Liter Volumeninhalt aus Hygienegründen ständig auf 60 °C gehalten. Geduscht wird aber wahrscheinlich nur mit einer Wassertemperatur von 40 °C. Wie viel Wasser von 40 °C kann entnommen werden, wenn man die Nachheizung mal komplett ausklammert? Das kalte Wasser des Versorgers soll mit 10 °C an der Duscharmatur zugemischt werden. Reicht der Speicherinhalt aus für ein zehnminütiges Spaßbrausen mit einem Durchsatz von 0,5 Liter pro Sekunde.
Beispiel 2:
Ein Heizkessel für Festbrennstoffe liefert ständig Vorlauftemperaturen von 90 °C. Die Fußbodenheizung soll für eine Vorlauftemperatur von 40 °C ausgelegt werden. bei einem Volumenstrom von 1200 kg/h. Die Rücklauftemperatur der Fußbodenheizung beträgt 30 °C. Welche Menge des umlaufenden Wassers wird dabei aus dem Rücklauf der Fußbodenheizung beziehungsweise dem heißen Vorlauf des Kessels zugemischt?
Diese Problemstellungen können per Formel oder per Mischungskreuz gelöst werden. Wir zeigen beide Wege.
Formelweg
Zuerst soll die Aufgabenstellung zu der Dusche im Einfamilienhaus gelöst werden.
Die Ausgangsformel zur Mischwasserberechnung ist
mm • ϑm = mk • ϑm + mw • ϑm
darin bedeutet:
- mm die Masse an gemischtem Wasser in Kilogramm [kg]
- ϑm die Temperatur des gemischten Wassers in Grad Celsius [°C]
- mk die Masse an Kaltwasser [kg]
- ϑk die Temp. des Kaltwassers [°C]
- mw die Masse an Warmwasser [kg]
- ϑw die Temp. des Warmwassers [°C]
Diese Ausgangsformel lässt sich mit einigem Geschick umstellen. Gesucht wird ja die Masse an Warmwasser, die für diesen Vorgang notwendig ist.

Gegeben ist:
mm = 0,5 l/s für zehn Minuten also
mm = 300 kg
ϑm = 40 °C
ϑk = 10 °C
ϑw = 60 °C
mw = gesucht
Für sehr viele Anwendungen in der Sanitärtechnik und dem Heizungsbau kann man ausreichend genau ein Kilogramm Wasser mit dem Volumen von einem Liter Wasser gleichsetzen.
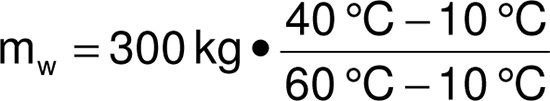
Für das zehnminütige Duschbad würden 180 Liter Wasser von 60 °C notwendig sein. Es müsste also eine Nachheizung erfolgen die gute 30 Liter innerhalb von 10 Minuten nachheizt oder es müsste eine höhere Wassertemperatur vorgehalten werden. Im Zweifel kann man natürlich auch das Speichervolumen anpassen.
Mischkreuzweg
Die Aufgabenstellung für den Lösungsansatz mit dem Mischungskreuz bleibt natürlich gleich.
mm = 300 kg
ϑm = 40 °C
ϑk = 10 °C
ϑw = 60 °C
mw = gesucht
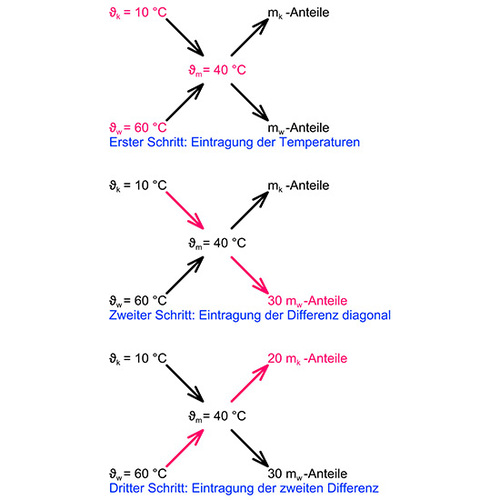
Man skizziert ein Kreuz das in der Mitte und an den linken Ecken Platzhalter hat für die angenommenen Temperaturen, wie im Bild gezeigt.
Dann rechnet man über Kreuz die Differenzen zwischen den Zahlen aus und trägt die Ergebnisse diagonal gegenüber ein. Und jetzt liest man bereits ein mögliches Ergebnis ab:
Das lautet:
Wenn man 30 Anteile Warmwasser von 60 °C nimmt und 20 Anteile Kaltwasser von 10 °C dazumischt ergibt dies ein Mischwasser von 40 °C.
Die beiden Massenanteile für kaltes und warmes Wasser ergeben zusammen 50 Anteile.
Gefragt war aber nicht nach 50 Anteilen sondern nach 300 kg des Mischwassers
Vorletzter logischer Schluss ist die Frage nach dem Gewicht von einem Anteil und der beträgt nun mal
300 kg / 50 Anteile = 6 kg/Anteil
Von den 6 kg/Anteil rechnet man nun ganz einfach wieder hoch auf 30 Anteile Warmwasser
also 30 Anteile • 6 kg/Anteil = 180 kg
und auf 20 Anteile Kaltwasser
also 20 Anteile • 6 kg/Anteil = 120 kg
Fazit und zweite Lösung
Mit dem Mischkreuz lässt es sich gut leben. Wer ohne Formelsammlung eine Aufgabe zum Thema Mischwasserberechnung lösen muss, der steht mit dem Mischungskreuz gut da. Für die zweite Aufgabe mit dem 90 °C heißen Kesselwasser und der Fußbodenheizung mit einer Vorlauf- bzw. Rücklauftemperatur von 40 bzw. 30 °C ergibt sich übrigens eine Masse von 1000 kg aus dem Rücklauf der Fußbodenheizung und entsprechend 200 kg aus dem Kessel. Aber prüfen Sie selbst. Weitere Aufgaben und Lösungenzum Thema Mischwasser finden Sie ab Seite 40 unter Fachwissen.






